094. Matura 1886 w zaborze austriackim. Zadanie z procentu składanego.
Posted by Mariusz Wdowiak on środa, sierpnia 29, 2018 with 4 comments
Jedno z najstarszych „ekonomicznych” zadań maturalnych,
jakie znalazłem pochodzi z roku 1886, czyli sprzed 132 lat. Polska była wówczas
pod zaborami, ale w zaborze austriackim matury odbywały się w języku polskim i
można o nich poczytać w sprawozdaniach dyrekcji poszczególnych szkół.
Maturzysta z roku 1886 patrząc na dane z tablicy bez trudu odczyta, że jeśli ulokujemy kapitał na 5% po 15 latach osiągnie on wartość 2,0789 kwoty bazowej i udziela poprawnej odpowiedzi.
Inne zadania z tamtych czasów są mocniejsze merytorycznie. Nie ma więc co mówić o C.K. zadaniach dla C.K. maturzystów! Jeszcze się o tym przekonacie...
We wrześniu 1886 roku na egzaminie maturalnym z matematyki
przeprowadzonym w cesarsko-królewskim IV Gminazjum we Lwowie (możliwe, że była
to matura o charakterze poprawkowym) znalazło się zadanie poświęcone procentowi
składanemu. Treść zadania, którą znalazłem w „Sprawozdaniu Dyrektora C.K.
Gimnazyum we Lwowie za rok szkolny 1887” (pisownia oryginalna), liczyła ledwie
dwanaście słów i mieściła się w jednym zdaniu, które brzmiało: Po ilu latach
podwoi się jakikolwiek kapitał dany na 5% składany?
Postarajmy się je rozwiązać.Analiza treści zadania.
Zadanie dotyczy właściwości procentu składanego i jako takie ma bardzo uniwersalny charakter. Świadczy o tym sformułowanie „jakikolwiek kapitał”. Bo wysokość kapitału pierwotnego oczywiście nie ma wpływu na okres, w którym stan oszczędności zwiększy się o określoną ilość razy.
Obraz wyłaniający się z zadania jest następujący: pieniądze
lokujemy na stały procent, który wynosi 5%. Raczej bezdyskusyjnie należy
przyjąć, że chodzi o oprocentowanie liczone w skali roku. Naliczone odsetki
będą kapitalizowane na rachunku lokaty. Pytanie brzmi: kiedy wartość lokaty
osiągnie dwukrotność kwoty bazowej.
Rozwiązanie absolutnie matematyczne.
Problem postawiony w treści zadania można wyrazić następującym równaniem:
gdzie K- kwota kapitału, r- oprocentowanie, n-okres
lokowania środków liczony w latach.
W przypadku naszego zadania należy rozwiązać następujące
równanie:
gdzie niewiadomą jest n – liczba lat. Równanie błyskawicznie przekształcamy do postaci:
I wszystko jasne. Ale tylko dla matematyka, bo każdy inny
człowiek zapyta „czyli ile to wynosi?”.gdzie niewiadomą jest n – liczba lat. Równanie błyskawicznie przekształcamy do postaci:
Odpowiedź zrozumiała dla wszystkich.
Odpowiedź, którą każdy zrozumie, i która prawdopodobnie byłaby zgodna z oczekiwaniami cesarsko-królewskiej komisyji egzaminacyjnej, wymaga podania liczby lat.
Mając dostęp do Excela, możemy skorzystać z funkcji
log(liczba;podstawa) i w ułamku sekundy przekonać, się, że
czyli mówiąc praktycznie: przy oprocentowaniu 5% na
podwojenie kapitału trzeba czekać 15 lat (dokładnie dwukrotność zostanie
osiągnięta po 14,2067 latach, czyli 14 latach, 2 miesiącach i 15 dniach, ale
bank i tak naliczać będzie odsetki w rocznicach założenia lokaty, więc trzeba
czekać do końca 15 roku).
Jak sobie radzili C.K. maturzyści z roku 1886?
Excela nie mieli. Za to mieli tablice matematyczne, z których mogli odczytać między innymi przyrost kapitału lokowanego w oparciu o procent składany. Dziś o tablicach matematycznych mało kto pamięta. Coraz trudniej jest je znaleźć w bibliotekach i na strychach. Ale nie ma co płakać, bo mając Excela można je sobie w kilkanaście sekund sporządzić. Proszę bardzo:Maturzysta z roku 1886 patrząc na dane z tablicy bez trudu odczyta, że jeśli ulokujemy kapitał na 5% po 15 latach osiągnie on wartość 2,0789 kwoty bazowej i udziela poprawnej odpowiedzi.
Jeśli miałby ochotę popatrzeć dłużej na dane z tablic to
odkryje, że gdyby oprocentowanie wynosiło 6%, to na podwojenie wartości
początkowego kapitału będziemy potrzebować jedynie 12 lat. Jeżeli natomiast
oprocentowanie byłoby mniejsze to okres podwajania kapitału będzie dłuższy i
wyniesie 18 lat (dla 4%), 24 lata (dla 3%) a w przypadku oprocentowania 1% i 2
% odpowiedź znajduje się na następnych stronach tablic...
Gdyby się okazało, że korzystanie z tablic jest zabronione, pozostaje liczenie na piechotę. Można sobie pomóc i ograniczyć liczbę operacji. Konkretnie: wiadomo, że po pierwszym roku kapitał wyniesie 1,05.Po dwóch latach będzie to iloczyn 1,05*1,05, czyli 1,1025. Jeżeli ten wynik podniesiemy do kwadratu uzyskamy wynik dla czwartego roku. Dwie kolejne takie same operacje (podniesienie uzyskanego wyniku do kwadratu) zaprowadzą nas do wartości przypisanej dla okresu 16 lat. Będzie większa niż 2 i trzeba się będzie cofnąć w obliczeniach. Dwa kroki w tył i znajdziemy odpowiedź na zadanie.
To wszystko jest jednak mocno rozczarowujące. Dokładnie jak
poziom tego zadania… Gdyby się okazało, że korzystanie z tablic jest zabronione, pozostaje liczenie na piechotę. Można sobie pomóc i ograniczyć liczbę operacji. Konkretnie: wiadomo, że po pierwszym roku kapitał wyniesie 1,05.Po dwóch latach będzie to iloczyn 1,05*1,05, czyli 1,1025. Jeżeli ten wynik podniesiemy do kwadratu uzyskamy wynik dla czwartego roku. Dwie kolejne takie same operacje (podniesienie uzyskanego wyniku do kwadratu) zaprowadzą nas do wartości przypisanej dla okresu 16 lat. Będzie większa niż 2 i trzeba się będzie cofnąć w obliczeniach. Dwa kroki w tył i znajdziemy odpowiedź na zadanie.
Inne zadania z tamtych czasów są mocniejsze merytorycznie. Nie ma więc co mówić o C.K. zadaniach dla C.K. maturzystów! Jeszcze się o tym przekonacie...


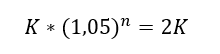


















Co do okresu podwojenia kapitału, bardzo dobre przybliżenie daje tzw. reguła 70. Otóż czas podwojenia kapitału to ok. 70/(100r) lat. Wynika to łatwo ze wzoru na zmianę podstawy logarytmu oraz rozwinięcia funkcji logarytmicznej w szereg Maclaurina. W realiach zadania będzie 70/5=14.
OdpowiedzUsuńNie znałem tej metody. Dziękuję za komentarz i za "rozwiązanie" przysłane mailem.
UsuńmencbiOre-da-Hartford Mike Arroyo https://marketplace.visualstudio.com/items?itemName=distmitrasto.Diorama-Tower-Defense--Tiny-Kingdom--Prologue--gratuita
OdpowiedzUsuńnamecolse
super
OdpowiedzUsuń